No post de hoje iremos construir, por semelhança, os conceitos de seno, cosseno, tangente, cotangente, secante e cossecante.
Olá queridos leitores. No post de hoje iremos construir, por semelhança, os conceitos de seno, co-seno, tangente, co-tangente, secante e co-secante. Neste post, estamos tratando de ângulos de 0 a 90º.
A trigonometria se assenta na semelhança de triângulos. Veja que, para que determinemos toda uma classe de triângulos retângulos semelhantes, basta conhecermos apenas um de seus ângulos, exceto o reto.
Veja que, por exemplo, no caso do triângulo retângulo que possui 30º como ângulo interno, como a soma dos ângulos internos de um triângulo qualquer é igual a 180º, estamos aqui falando de Geometria Euclidiana, o terceiro ângulo só pode ser 60º, pois 30º+90º+60º=180º. Então, todos os triângulos retângulos que possuem o ângulo de 30º são semelhantes pelo caso ângulo ângulo. Isto significa que os lados entre os mesmos ângulos são proporcionais.
Mas, e o seno?
Voltemos ao ângulo de 30º. Como os infinitos triângulos retângulos que possuem o ângulo interno de 30º têm lados homólogos proporcionais, encontraremos situações que resultam em valores invariáveis. Por exemplo, sempre que dividirmos o cateto oposto a 30º pela hipotenusa, sempre teremos o valor 1/2, não importando qual dos infinitos triângulos retângulos semelhantes que possuem o ângulo interno de 30º escolhermos. Esta razão é chamada de seno. Cada ângulo, aqui estamos falando de ângulos de 0º a 90º, tem um valor único de seno.
Mas, e o co-seno?
Ainda trabalhando com os infinitos triângulos retângulos semelhantes, que têm como ângulos internos 30º, 90º e 60º, vamos mover a nossa atenção ao ângulo de 60º. Observe que o que era cateto oposto a 30º, passa a ser cateto adjacente a 60º, e, claro, quando se divide o cateto adjacente a 60º pela hipotenusa obtemos o mesmo valor 1/2, para qualquer um dos infinitos triângulos semelhantes com ângulos internos 30º, 90º e 60º que escolhermos. Esta razão é chamada de co-seno. Cada ângulo, aqui estamos falando de ângulos de 0º a 90º, tem um valor único de co-seno.
Em ângulos complementares, o seno de um é o co-seno do outro e vice versa
Veja que o seno de 30º é o cosseno de 60º e vice versa. Isto acontece porque 30º e 60º fazem parte dos infinitos triângulos retângulos semelhantes, que possuem 30º, 90º e 60º como ângulos internos. Logo, o cateto oposto a 30º é o cateto adjacente a 60º e vice versa. Você pode explorar esta ideia neste aplicativo do GeoGebra,
clique aqui para acessá-lo).
 |
| Observe que o programa GeoGebra trabalha com arredondamento |
Tangente, co-tangente, secante e co-secante de teta, de onde vêm?
Vamos ao círculo trigonométrico para encontrar, com a semelhança de triângulos, a tangente, a co-tangente, a secante e a co-secante de um ângulo...
Vamos partir do seno e do co-seno de teta
Veja que, no círculo trigonométrico, o raio é 1, e a hipotenusa, que é um dos raios do círculo trigonométrico, tem justamente esta medida. Logo, o seno, no círculo trigonométrico pode ser calculado diretamente pela medida do cateto oposto ao ângulo teta uma vez que seno de teta=cateto oposto/hipotenusa, e como a hipotenusa vale 1, seno de teta=cateto oposto. O mesmo vale para o cosseno.
Veja que aqui o eixo horizontal é chamado eixo dos cossenos e o eixo vertical é chamado eixo dos senos. Veja que, o círculo trigonométrico permite que percebamos que os valores do seno de teta, no primeiro quadrante, só poderão variar de 0 a 1, o mesmo acontecendo para o cosseno de teta neste mesmo quadrante.
Observe que a identidade trigonométrica fundamental sen²teta+cos²teta=1 é obtida aqui por meio do teorema de Pitágoras.
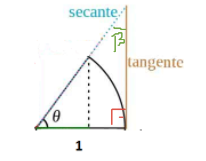
Nascem as fórmulas da tangente e da secante de teta
Continuando, veja que prolongando a hipotenusa, interceptamos a reta que é tangente ao círculo trigonométrico em 0º e 360º. Construímos assim, um segundo triângulo, semelhante ao triângulo que possui seno e cosseno de teta como catetos.
Utilizando a semelhança de triângulos obtemos a fórmula da tangente de teta e a fórmula da secante de teta.
Nasce a fórmula da tangente de teta
tg teta/sen teta=1/cos teta, daí, tg teta=sen teta/cos teta, logo, temos tg teta= (cateto oposto/hipotenusa)/(cateto adjacente/hipotenusa), daí tg teta= cateto oposto/cateto adjacente.
Nasce a fórmula da secante de teta
sec teta/1=1/cos teta, daí, sec teta= 1/cos teta.
Nascem as fórmulas da co-tangente e da co-secante de teta
Continuando, veja que prolongando a hipotenusa, interceptamos a reta que é tangente ao círculo trigonométrico em 90º (esta reta é chamada cotangente). Construímos assim, um terceiro triângulo, semelhante ao triângulo que possui seno e cosseno de teta como catetos e ao triângulo que possui secante e tangente de teta como catetos.
Girando este triângulo, cujos catetos são a co-tangente de teta e a co-secante de teta, visualizamos melhor a sua semelhança com os triângulos anteriormente mencionados. Agora estamos prontos para encontrar, utilizando semelhança de triângulos, as fórmulas da co-tangente de teta e da co-secante de teta.
Nasce a fórmula da co-tangente de teta
co-tg teta/cos teta=1/sen teta, daí co-tg teta = cos teta/sen teta, logo co-tg teta = cateto (adjacente/hipotenusa)/ (cateto/oposto/hipotenusa), então co-tg teta= cateto adjacente/cateto oposto.
Nasce a fórmula da co-secante de teta
co-sec teta/1=1/sen teta, daí, co-sec teta = 1/sen teta.
Considerações finais
Construir as razões trigonométricas seno, cosseno, tangente, co-tangente, secante e co-secante por semelhança mostra ao estudante que é possível desenvolver conceitos geométricos sem memorização, isto é fundamental para o seu aprendizado.
A autora
Daniela Mendes é doutora pelo programa de pós graduação em Ensino de Matemática da UFRJ, leciona Matemática no Ensino Médio (SEEDUCRJ) e no Ensino Superior (UERJ). É também professora dos cursos de formação continuada da Fundação CECIERJ para professores de Matemática. Coordena, no Colégio Estadual Hebe Camargo, desde 2014, o projeto Laboratório Sustentável de Matemática.